目录 6
第一章 简介 11

第二章 笛卡尔坐标系统 14

1. 研究自然数和整数的领域称作离散数学，研究实数的领域称作连续数学。而物理学家认为实数只是一种错觉，因为宇宙是离散和有限的。

2. 计算机图形学第一准则：近似原则如果它看上去是对的它就是对的。

第三章 多坐标系 27

1. 世界坐标系

2. 物体坐标系

3. 摄像机坐标系

4. 惯性坐标系
   

   惯性坐标系的原点和物体坐标系的原点重合，但惯性坐标系的轴平行于世界坐标系的轴。
   

第四章 向量 36

1. 任意一点都能用从原点开始的向量来表达

第五章 向量运算 44

1. 数学中专门研究向量的分支称为线性代数
   

2. 向量点乘

   得标量
   

3. 向量叉乘

   叉乘向量垂直于原两个向量

第六章 3D向量类 67

第七章 矩阵 79

1. 矩阵——数学定义

   以行列形式组织的矩形数字块 

1. 方阵、对角矩阵、单元矩阵（I，矩阵的乘法单位元）

2. 行向量、列向量

3. 转置，沿对角线翻折

   

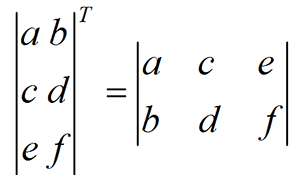
4. 标量与矩阵乘法

5. 矩阵乘法

   

1. 矩阵与方阵相乘，得到的矩阵大小与原矩阵相同

2. 矩阵乘法不满足交换律

3. 矩阵乘法满足结合律：

   结合律计算中有些扩法的标量计算更少——矩阵链问题

4. 矩阵乘法也满足与标量或向量的结合律

5. 矩阵积的转置相当于先转置矩阵再以相反的顺序乘：

6. 向量与矩阵的乘法

   

1. 满足向量加法的分配律：

7. 行向量与列向量

1. 推荐使用行向量

2. 矩阵——几何解释

1. 旋转、缩放、投影、镜像、仿射

2. 矩阵的每一行都能解释为转换后的基向量。

   

   2D变换：
   

   

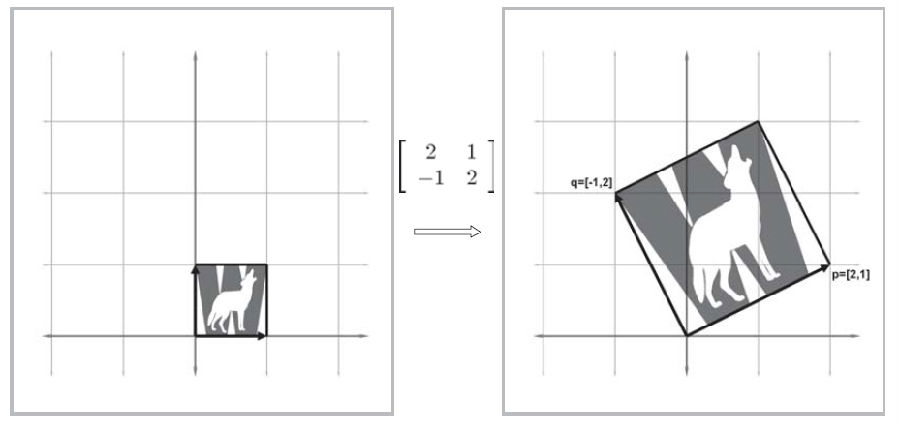
   3D变换：

   

第八章 矩阵和线性变换 95

第九章 矩阵的更多知识 119

第十章 3D中的方位与角位移 140

第十一章 C++实现 184

第十二章 几何图元

第十三章 几何检测

第十四章 三角网络

第十五章 图形数学

第十六章 可见性检测

第十七章 后记

附录A 简单的数学概念

附录B 参考文献